Extra Homework

(do not turn in)

Description

In Section 3 of [Tsuchiya88a], the author gave a brief description of a hierarchy management algorithm which is used to build a hierarchy of Landmarks from the bottom up. Your job is to:

1. Write out such an algorithm in detail.
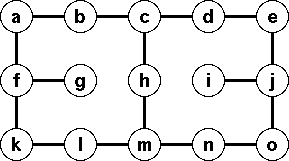
2. Apply your algorithm to the physical network shown below assuming that the radius of a level n landmark router is 2^(n+1) (2 raised to the power of n+1).

Requirements

1. Prepare a detailed description of your hierarchy management algorithm. You may find proposed solutions to this problem by searching the Internet. If you find such a proposal, you may not simply copy the algorithm and turn it in. In this case, you must study the algorithm and understand it throughly and describe the algorithm in your own words. If your solution comes from such a souce, you must also cite your source.
2. For part (2), please write down your answers in a table with the following columns:
   • original name (i.e., a, b, c, ... in alphabetical order)
   • new name
   • (landmark) level
   • orignal names of landmarks visible in routing table (you do not need to write down level and nexthop values)

Hints

If you are stuck, [Estrin99a] may have some helpful hints.

Description

Let the physical network topology be as shown above. Furthermore, let the radius of a level n landmark router is 2^(n+1) (2 raised to the power of n+1.

Questions

1. What's the minimum number of LM1 router(s) you must have?
2. Continue from part (1), which LM0 router(s) will you promote to be LM1 router(s) to achieve this minimum?
3. What's the minimum number of LM2 router(s) you must have?
4. Continue from part (3), which LM1 router(s) will you promote to be LM2 router(s) to achieve this minimum?
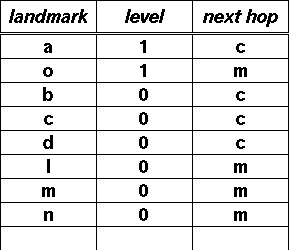
5. Continue from part (4), please write down the routing table at node h.

Anaswers

1. three
2. a, h, and o
3. one
4. h
5.  

   

Description

Solve the WFQ problem on slide 33 of lecture 15.

• Three input queues, X, Y, and Z. Their weights are 1, 2, and 1, respectively.
• Packet sizes are identical and equal to 1.
• Packet arrivals are as follows.
  • At real time 1, one packet (X1) arrives at queue X and onen packet (Z1) arrives at queue Z.
  • At real time 2, one packet (Y2) arrives at queue Y.
  • At real time 3, one packet (X3) arrives at queue X.
  • At real time 4, one packet (Z4) arrives at queue Z.
  • At real time 5, one packet (Y5) arrives at queue Y.

Requirements

• Using Weighted Fair Queueing, what are the (logical) arrival times and the (logical) finish times of these six packets? Please show your calculations.

  Please use the notation A[P#] and F[P#] for the arrival time and finish time of packet P#.

• In what order are the packets being sent out by the output queue? In case of a tie, please give queue X priority over queue Y, and queue Y over queue Z.

Solution

• A detailed solution is provided here.